Diese Seite funktioniert nur mit Javascript.
Elastizitäten2.4.1 ElastizitätsbegriffSpezifische Elastizitäten
lastizitätswerte vermitteln Ökonomen Informationen, wie "heftig" oder "stark" eine Größe auf eine andere reagiert. Wenn sie sich unterhalten, müssen sie sich meistens gar nicht verständigen, von welcher der zahlreichen Elastizitäten sie gerade reden. Oft nennen sie auch keine exakten Werte, sondern formulieren solche Sätze wie "Die Nachfrage reagiert unelastisch". Auch ob ein Elastizitätswert positiv oder negativ ist, erwähnen sie meist nicht. Trotzdem weiß jeder, was der andere meint. Aus dem Zusammenhang wird meist klar, von welcher Elastizität gerade die Rede ist. Auch die Vorzeichen der Elastizitäten sind in aller Regel von vornherein bekannt. Deswegen werden sie nur erwähnt, wenn sie nicht den Erwartungen entsprechen. Und für theoretische Überlegungen ist es oft nur wichtig zu wissen, ob die Elastizitäten bestimmte Grenzwerte über- oder unterschreiten. Der exakte Wert ist weniger von Bedeutung.
Das Ökonomendeutsch "Die Nachfrage reagiert unelastisch" heißt übersetzt: "Wenn der Preis des Gutes um ein Prozent steigt, wird die Nachfrage um weniger als ein Prozent zurückgehen." Eine ähnliche Aussage lässt sich für jede Elastizität $y$ bzgl. $x$ formulieren: Wenn der Wert der unabhängigen Variable $x$ um ein Prozent steigt, ändert sich der Wert der abhängigen Variable $y$ um soundsoviel Prozent.
Angenommen, ein Betrieb hat seine Beschäftigung von einem auf den anderen Monat von 400 auf 416 Mitarbeiter erhöht und die Produktion ist dadurch - ceteris paribus versteht sich - von 1500 auf 1530 Stück angestiegen. Dann kann eine Elastizität der Produktionsmenge bzgl. der Beschäftigung in drei Schritten berechnet werden:
- Schritt 1: Die Produktion $Q$ ist um 2 Prozent gestiegen.
- Schritt 2: Die Beschäftigung $B$ ist um 4 Prozent gestiegen.
- Schritt 3: Je ein Prozent Beschäftigungsanstieg ist die Produktion um 0,5 Prozent gestiegen.
Die Elastizität der Produktion bzgl. der Beschäftigung $E_{\text{Produktion,Beschäftigung}}$ ist 0,5 - oder kurz $E_{Q,B} = 0,5$. Da die prozentualen Veränderungen, aus denen die Elastizität berechnet wird, dimensionslos sind, ist auch der Elastizitätswert selbst dimensionslos. Also eigentlich eine simple Angelegenheit: etwas Prozentrechnung und ein einfacher Dreisatz.
Den Wert der Elastizität können wir einschätzen: ein Prozent mehr Beschäftigte führt zu einem halben Prozent mehr Produktion. Wir haben ein Gefühl dafür, ob das viel oder wenig ist. Jedenfalls gewinnen wir aus dieser Maßzahl mehr Information als aus der Aussage, dass 16 zusätzliche Mitarbeiter die Produktion um 30 Stück haben steigen lassen. Das ist nämlich sehr wenig, wenn zuvor ein Mitarbeiter allein schon 30 Stück produziert hat, und es ist sehr viel, hätten zuvor 100 Mitarbeiter 30 Stück produziert.
Die Möglichkeit, an Elastizitätswerten sofort erkennen zu können, ob ein Zusammenhang stark oder schwach ausgeprägt ist, fehlt, wenn nur absolute Änderungen bekannt sind. Wenn man keine Vorstellung hat, was eine Tonne Koks kostet und wie viel Tonnen Koks in Deutschland in einem Jahr gehandelt werden, dann kann man mit der Information, dass der Preis für eine Tonne Koks um 100 DM gestiegen und daraufhin die Nachfrage um 250 Tonnen zurückgegangen ist, nichts anfangen. Kennt man aber den entsprechenden Elastizitätswert, wird die Information wesentlich gehaltvoller. So würde ein Wert von 0,1 anzeigen, dass die Nachfrage bei einer einprozentigen Preissteigerung um 0,1 Prozent zurückgehen würde. Eigentlich ein Elastizitätswert von -0,1, aber das Vorzeichen wird - wie gesagt - wenn die Richtung des Zusammenhangs klar ist, meist unterschlagen.
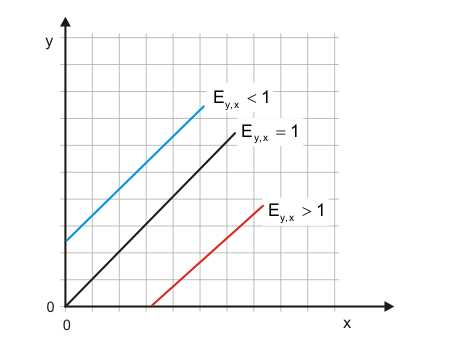
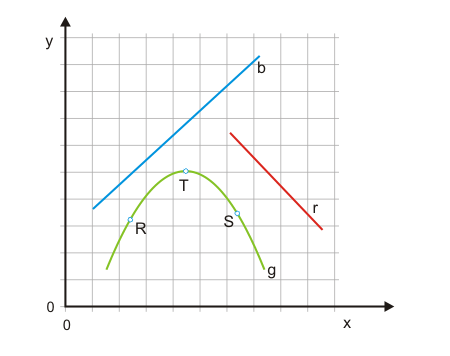
In Abbildung 1 wird gelöst von inhaltlichen Zusammenhängen betrachtet, wie die Größe x die Größe y beeinflusst. Für die verschiedenfarbigen Funktionen gilt:
- Die blaue Funktion (b) besitzt durchgängig eine positive Elastizität, denn wenn x steigt, steigt auch y.
- Die rote Funktion (r) zeigt durchgängig eine negative Elastizität.
- Die grüne Funktion (g) besitzt in R eine positive und in S eine negative Elastizität. In T besitzt sie eine Elastizität von null.
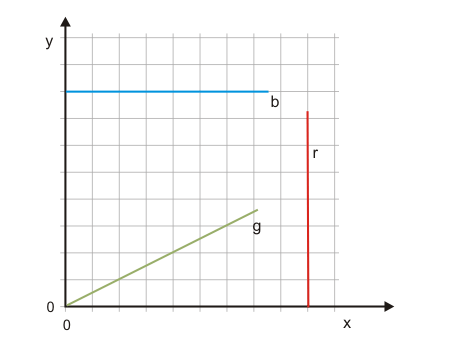
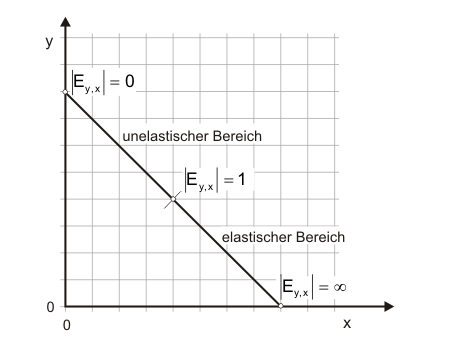
Man kann also aus der Steigung der Funktion auf das Vorzeichen der Elastizitäten schließen. Das gilt allerdings nur, wenn beide Werte $x$ und $x$ positiv sind, was bei ökonomischen Anwendungen aber regekmäßig der Fall ist. Den Wert der Elastizität kann man aber aus der Steigung allein nicht ablesen. Geraden sind bis auf drei Ausnahmen Funktionen, Funktionen mit unterschiedlichen Elastizitäten. Abbildung 2 zeigt die drei Ausnahmen. Funktionen mit konstanter Elastizität heißen isoelastisch.
Die grüne Gerade (g) besitzt durchgängig eine Elastizität von eins, die rote Gerade (r) von unendlich und die blaue Gerade (b) von null. Das macht man sich für die beiden letzten Fällen mit der Überlegung klar, wie Änderungen des Wertes $x$ den Wert $y$ beeinflussen. Die grüne Gerade lässt - da sie durch den Ursprung verläuft - das Verhältnis von $x$ und $y$ in jedem Punkt konstant. Also ändern sich $x$ und $y$ proportional zueinander. Wenn $x$ um ein Prozent steigt, dann muss auch $y$ um ein Prozent steigen (sonst würde sich das Verhältnis ändern). Also ist die Elastizität eins.
In einem Marktdiagramm würde man die blaue Gerade vollkommen elastisch und die rote Gerade vollkommen unelastisch nennen. Widerspricht das nicht den Ausführungen im letzten Absatz? Wenn Sie's nicht wissen - hier finden Sie die Antwort.
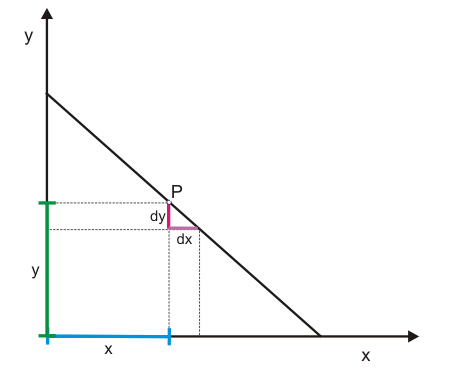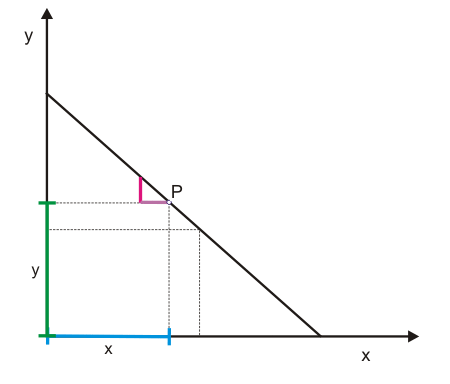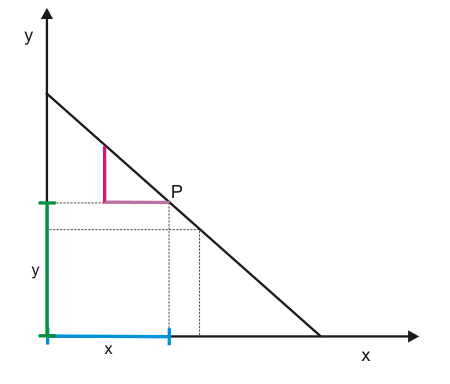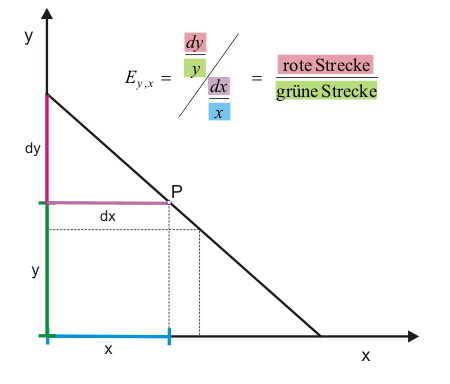
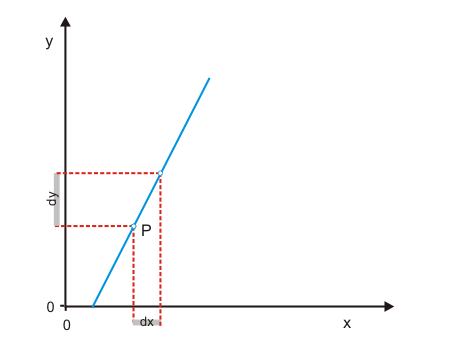
Dabei bezeichnet $dy$ die Veränderung des Wertes von $y$, der durch die Veränderung $dx$ des Wertes von $x$ ausgelöst wird. Wenn man Zähler und Nenner jeweils mit 100 multipliziert, erkennt man die verbale Definition in der Formel wieder
$$E_{y,x}=\cfrac{\cfrac{dy}{y}\cdot100}{\cfrac{dx}{x}\cdot100}=\cfrac{\text{Prozentuale Änderung von y}}{\text{Prozentuale Änderung von x}}\tag{2}$$Da die prozentualen Änderungen nichts anderes sind als Wachstumsraten, kann man auch sagen, Elastizitäten sind das Verhältnis zweier Wachstumsraten.
Den folgenden Satz sollten Sie auswendig lernen - es lohnt sich:
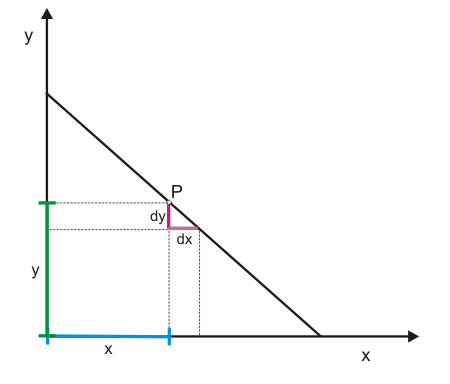
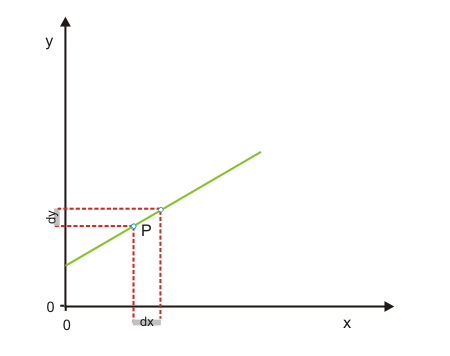
Mithilfe der Abbildungen 3 und 4 wird gezeigt, wie man die Elastizität einer fallenden Gerade grafisch ermitteln kann. Dazu wird in Abbildung 3 ausgehend von P eine Änderung $dx$ angenommen, die eine Änderung $dy$ bewirkt. Die Ausgangswerte von $x$ und $y$ lassen sich als blaue und grüne Strecke erkennen. Die Strecken $dy$ und $dx$ in Abbildung 3 verhalten sich zueinander wie die Strecken $dy$ und $dx$ in Abbildung 4. Im Punkt P wird die Elastizität $E_{y,x}$ daher durch das Verhältnis der roten zur grünen Strecke angezeigt (die blaue Strecke x und die lilafarbene Strecke $dx$ sind gleich lang und können daher in der Formel gegeneinander gekürzt werden). Sie liegt damit knapp unter eins. Wäre P genau auf halber Strecke der Geraden gelegen, betrüge die Elastizität exakt eins.
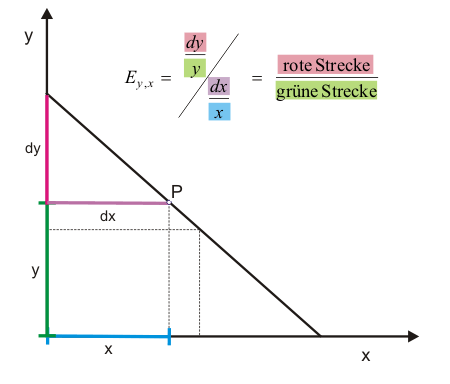
Eigentlich ist die Elastizität hier negativ, denn die positive Änderung bei $x$ löst eine negative Änderung bei $y$ aus. Wenn man also korrekt sein wollte, müsste man eigentlich von absoluten Werten sprechen. Die Elastizität ist also auf halber Strecke der Geraden minus eins bzw. der absolute Wert der Elastizität ist eins.
Wenn der Wert der Elastizität absolut über eins liegt, nennt man den Zusammenhang elastisch. Liegt der Wert unter 1, nennt man ihn unelastisch. Wenn der Wert gegen unendlich geht, spricht man von einem vollkommen elastischen Zusammenhang. Hat eine Elastizität den Wert null, nennt man den Zusammenhang vollkommen unelastisch.
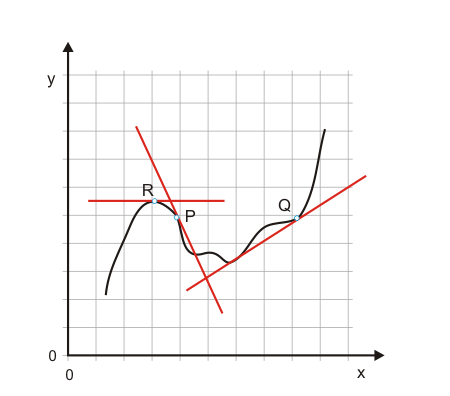
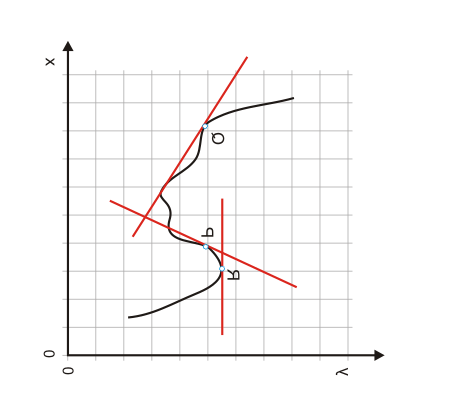
Wenn man die Elastizität $E_{y,x}$ einer Kurve in einem bestimmten Punkt ermitteln möchte, ermittelt man die Elastizität der Tangente an diesen Punkt. In Abbildung 5 erkennt man somit für den Punkt R eine Elastizität von null, für P eine negative und für Q eine positive Elastizität. Die Elastizität $E_{x,y}$ ist der Kehrwert von $E_{y,x}$. Einen optischen Eindruck gewinnt man durch Drehen und Spiegeln des Diagramms (s. Abb. 5).
Wie für eine fallende Gerade kann man auch für eine ansteigende Gerade die Elastizität grafisch bestimmen. Prinzipiell unterscheidet sich die Vorgehensweise nicht, so dass auf eine Wiedergabe verzichtet wird. Abbildung 6 zeigt bereits das Ergebnis. Die Elastizität $E_{x,y}$ im Punkt P kann abgelesen werden als das Verhältnis der Strecke 0B zur Strecke AB.
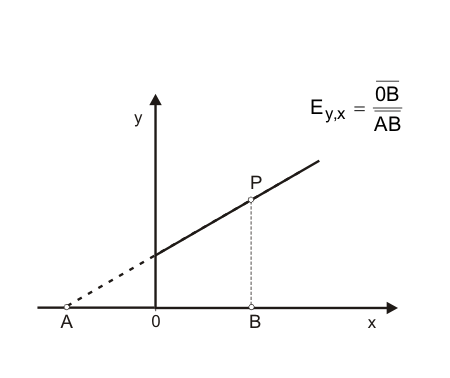
Den Schnittpunkt mit der Abszisse muss man wie in diesem Beispiel u. U. durch Verlängern der Gerade finden. Da AB hier länger als 0B ist, kann für P eine Elastizität kleiner eins festgestellt werden. In P ist die Funktion also unelastisch. Aber auch in allen anderen Punkten, da immer AB > 0B gilt.
Wenn eine Gerade durch den Ursprung geht, fällt A mit dem Ursprung zusammen und es gilt 0B = AB. Also besitzt jede Gerade durch den Ursprung eine Elastizität von eins, was ja bereits weiter oben anhand der Plausibilitätsüberlegung gezeigt wurde, dass auf einer Geraden durch den Ursprung das Verhältnis $x$ zu $y$ konstant bleibt. Wenn A die Abszisse im positiven Bereich schneidet, besitzt die Gerade in jedem Punkt eine Elastizität größer eins.
Wenn man Elastizitäten berechnen möchte, bietet sich eine Umformung von Gleichung (1) an.
$$E_{y,x}={\cfrac{dy}{dx}}\cdot{\cfrac{x}{y}}\tag{3}$$an. Der Bruch vor dem Malzeichen zeigt die Steigung, die mit dem Verhältnis von x zu y multipliziert wird (s. a. Abb. 4). Die Elastizität der Funktion $y=3x^2$ lässt sich damit für $x=2$ wie folgt berechnen:
$$y=3x^2\tag{4}$$ $$y(x=2)=3\cdot2^2=12\tag{5}$$ $$\cfrac{dy}{dx}=2\cdot3x\tag{6}$$ $$E_{y,x}={\cfrac{dy}{dx}}\cdot{\cfrac{x}{y}}=2\cdot3\cdot2\cdot\cfrac{2}{12}=2\tag{7}$$Das glatte Ergebnis ist kein Zufall, wie folgende Berechnung zeigt:
$$y=ax^c\tag{8}$$ $$\cfrac{dy}{dx}={ac}\cdot{x^{c-1}}\tag{9}$$ $$E_{y,x}={\cfrac{dy}{dx}}\cdot{\cfrac{x}{y}}={ac}\cdot{x^{c-1}}\cdot\cfrac{x}{ax^c}=c\tag{10}$$Abschließend zeigt die Animation Abbildung 7 den Vergleich zweier Funktionen hinsichtlich ihrer Elastizität im gemeinsamen Punkt P und die Abbildungen 8 und 9 fassen einige der Ergebnisse zusammen.