Grenznutzen und Unsicherheit

2.2.3 Indifferenzkurven

Die Grenzrate der Substitution

m vorigen Abschnitt wurde unterstellt, man könne Nutzen messen. Diese Annahme ist unrealistisch und wird hier aufgegeben. Wie sich in diesem und dem folgenden Abschnitt zeigen wird, lässt sich auch ohne diese restriktive Annahme die Nachfragefunktion nach Gütern ableiten. Naturgemäß wird die Analyse dadurch etwas schwieriger. Das entscheidende analytische Instrument, das den Verzicht auf die kardinale Nutzenmessung ermöglicht, ist die Indifferenzkurve. Indifferenzkurven sind die grafischen Darstellungen von Nutzenfunktionen. Da Nutzenfunktionen Präferenzordnungen abbilden, geben Indifferenzkurven auch Auskunft über die Präferenzen eines Wirtschaftssubjekts. Man kann sagen, Indifferenzkurven sind das Bild der Präferenzen eines Wirtschaftssubjektes.

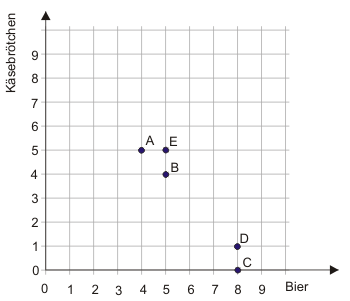
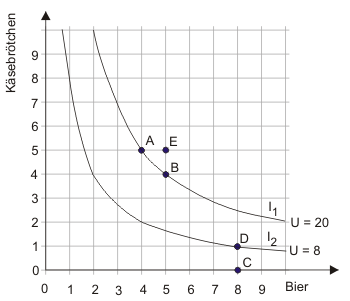
Zur Einführung von Indifferenzkurven führen wir das Käsebrötchen-Bier-Beispiel fort. Die fünf Güterbündel, über die der Haushalt die Präferenzordnung $E \succ A \sim B \succ D \succ C$ hat, sind in Abbildung 1 wiedergegeben.

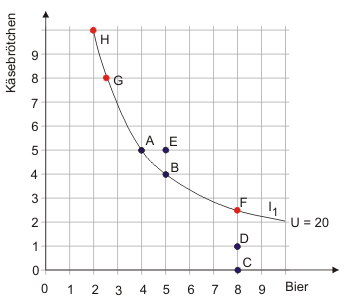
Aus der Präferenzordnung ist bekannt, dass der Haushalt zwischen den beiden Güterbündeln $A$ und $B$ indifferent ist, m.a.W. er findet sie gleich gut. In der Nutzenfunktion $U =K \cdot B$, die sich im vorletzten Abschnitt als geeignet erwiesen hat, die Präferenzordnung abzubilden, führen beide Güterbündel zu einem Wert von 20. Es gibt noch weitere Güterbündel, die zu einem Wert von 20 führen; z.B. das Güterbündel 2 Käsebrötchen, 10 Bier oder das Güterbündel 10 Käsebrötchen, 2 Bier. Wenn Käsebrötchen und Bier als teilbar angesehen werden, existieren unendlich viele Güterbündel, die zu einem Nutzenindexwert von 20 führen; z.B. Bündel $G$, das aus 2,5 Bier und 8 Käsebrötchen besteht. Alle Güterbündel mit gleichem Nutzenindexwert sind in Abbildung 2 durch die Kurve I₁ erfasst.

Nun ist davon auszugehen, dass der Haushalt zwischen den Güterbündeln $A, B, F, G$ und $H$ und allen anderen Güterkombinationen auf der Indifferenzkurve indifferent ist. Wenn das nicht zuträfe, dann müsste er eine andere Präferenzordnung haben, die durch die Nutzenfunktion $U =K \cdot B$ nicht zutreffend beschrieben wäre. Aber es spielt keine Rolle, wie die Präferenzordnung des Haushalts aussieht. Denn zu jeder Präferenzordnung lässt sich eine Nutzenfunktion finden. Und für jede Nutzenfunktion lässt sich für ein gegebenes Güterbündel ein Nutzenindexwert bestimmen, der dann über eine Indifferenzkurve alle anderen Güterbündel anzeigt, die in der Präferenzordnung des Haushalts den gleichen Rang einnehmen.

Nun gibt es natürlich nicht nur Güterbündel, die der Haushalt genau so gut wie $A$ findet, sondern auch solche, die er genau so gut wie $D$ findet. Wir wenden das Konstruktionsprinzip einer Indifferenzkurve nun an, indem wir alle Kombinationen von Käsebrötchen und Bier suchen, die zum gleichen Nutzenindexwert wie $D$ in Höhe von 8 führen und erhalten eine zweite Indifferenzkurve I₂ (s. Abb. 3). Von den beiden eingezeichneten Indifferenzkurven wissen wir, dass der Haushalt die Güterbündel auf der Indifferenzkurve I₁ besser findet als die Güterbündel auf I₂.

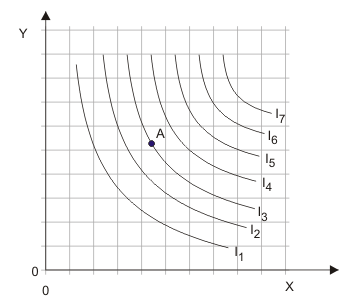
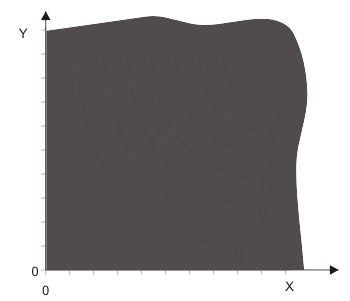
Da eine der Annahmen über die Präferenzordnung des Haushalt lautet, er könne jedes beliebige Güterbündel beurteilen, muss für jeden beliebigen Punkt im Diagramm - jeder Punkt entspricht einem Güterbündel - ein Nutzenindexwert bestimmbar sein. Also verläuft auch durch jeden Punkt im Diagramm eine Indifferenzkurve. Wenn man sie alle einzeichnen würde, sähe das so aus wie in Abbildung 4. Da man so aber nichts erkennen kann, beschränkt man sich darauf, einige ausgewählte Indifferenzkurven aus der Schar unendlich vieler Indifferenzkurven einzuzeichnen.

Für den betrachteten Haushalt gilt anscheinend, dass in seinen Augen bessere Güterbündel auf höheren Indifferenzkurven liegen (s. Abb. 3). Abgesehen von den beiden Achsen des Diagramms, erreicht der Haushalt eine höhere Indifferenzkurve (= höherer Nutzenindexwert = bevorzugtes Güterbündel), wenn man sich im Diagramm nach rechts oder nach oben (oder zugleich nach rechts und oben) bewegt. Das bedeutet, der betrachtete Haushalt zieht ein Güterbündel, das mehr Güter als ein anderes enthält, dem anderen vor.

Es ist sehr plausibel, dass Haushalte im allgemeinen mehr Güter weniger Gütern vorziehen werden. Wenn es umgekehrt wäre, müssten wir dann nicht beobachten, wie die Menschen Güter verschenkten? Wie sie sich über ihren Reichtum beklagen würden? Wie sie gerne mehr Steuern bezahlten? So ist es sicher nicht. Ganz im Gegenteil: Sie würden gerne im Lotto gewinnen, möchten bei gleicher Leistung gern mehr verdienen, würden gern günstiger einkaufen. Und das deutet alles darauf hin, dass sie sich mehr Güter leisten können möchten. Der Einwand, die Menschen möchten höherwertige anstatt mehr Güter, bereitet der Theorie keine Schwierigkeiten. Dazu definiert sie die Güter einfach um und die Haushalte fragen nicht Klein-, Mittel- und Luxuswagen, sondern "Autoeinheiten" nach. Ein Kleinwagen reicht dann z. B. bis 1000 Einheiten und ein Luxuswagen beginnt bei 5000 Einheiten. Und wer möchte nicht gerne von einem 2000-Einheiten-Auto auf ein 4000-Einheiten-Auto umsteigen?

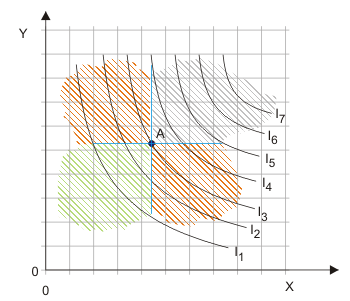
In Abbildung 5 ist ausgehend vom Güterbündel $A$ angezeigt, wo aufgrund der Nichtsättigungsannahme, Güterbündel liegen, die auch ohne Kenntnis der Präferenzordnung als besser oder schlechter als $A$ eingestuft werden können: Im grauen Bereich liegen alle besseren, im grünen Bereich alle schlechteren Güterbündel. Nur in den beiden roten Bereichen können Güterbündel liegen, die der Haushalt gleich gut wie $A$ findet. Die Indifferenzkurve, die durch $A$ verläuft, muss daher von links oben nach rechts unten verlaufen. Das gilt aber für jeden beliebigen anderen Ausgangspunkt auch, sodass Indifferenzkurven aufgrund der Nichtsättigungsannahme fallenden Verlauf haben.

Eine weitere wichtige Eigenschaft von Indifferenzkurven folgt aus der Transitivitätsannahme:

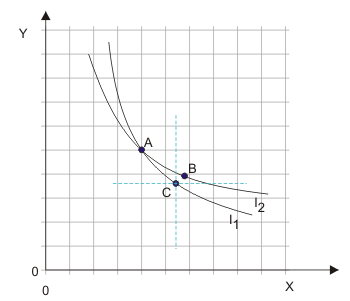
Um das zu sehen, gehen wir in Abbildung 6 vom gegenteiligen Fall aus. Danach ist der Haushalt indifferent zwischen $A$ und $B$, denn die beiden Güterbündel liegen auf der gleichen Indifferenzkurve. Aus dem selben Grund ist der Haushalt auch indifferent zwischen $A$ und $C$. Gilt die Transitivitätsannahme, ist der Haushalt zwischen $B$ und $C$ indifferent. Alle indifferenten Güterbündel liegen definitionsgemäß auf einer Indifferenzkurve. $B$ und $C$ liegen jedoch auf unterschiedlichen Indifferenzkurven. Also können sich Indifferenzkurven nicht schneiden. Zudem würde dies auch der Nichtsättigungsannahme widersprechen, derzufolge $B$ besser als $C$ ist, da $B$ von beiden Gütern mehr enthält.

Fassen wir die zentralen Ergebnisse dieser Seite noch einmal zusammen:

Eine weitere wichtige Eigenschaft von Indifferenzkuven lernen Sie im nächsten Abschnitt kennen:

Nach ähnlichen Seiten im WWW suchen