Diese Seite funktioniert nur mit Javascript.
Messung der Monopolmacht4.2.1.6 Messung der AnbieterkonzentrationMonopolistische Preisdifferenzierung
ur Messung der Anbieterkonzentration haben sich vor allem zwei Maße durchgesetzt: der Konzentrationsgrad und der Herfindahl-Index. Dass diese beiden es unter den zahlreich zur Auswahl stehenden Maßen zur Messung von Konzentration zu besonderer Popularität gebracht haben, liegt sicher nicht zuletzt an ihrer einfachen Berechenbarkeit, ihrer einfachen Interpretation und der Tatsache, dass sie auch von der Monopolkommission und vom Statistischen Bundesamt eingesetzt werden.
Typischerweise setzen die Maße am Umsatz der Unternehmen an. Aber ohne Weiteres könnte man z.B. auch die Beschäftigten, die Gewinne oder andere (quantitativ messbare) Merkmale x heranziehen. Zur Berechnung der Konzentrationsrate ist es zunächst notwendig, die Merkmale der Größe nach zu ordnen:
$$ x_1 > x_2 > x_3 > x_4 \space ... > x_n \tag{1} $$Mit der Summe $X$ der Merkmale aller $n$ Unternehmen
$$ X = \sum_{i=1}^n x_i \tag{2} $$werden die Anteile ai der Unternehmen berechnet:
$$ a_i = \cfrac{x_i}{X} \tag{3} $$Wird also z.B. der Umsatz betrachtet, so zeigt $a_i$ den Anteil, den Unternehmen $i$ am gesamten Marktumsatz hat.
Die Konzentrationsrate $\text{CR}_\text{j}$ ist dann einfach als Summe der Marktanteile der $j$ (gemessen am zugrunde gelegten Kriterium) größten Unternehmen definiert:
$$ \text{CR}_\text{j} = \sum_{i=1}^j a_i \tag{4} $$Ein Zahlenbeispiel, in dem 25 Unternehmen in einem Markt insgesamt 5.000 Einheiten Umsatz erzielen, verdeutlicht die Berechnung:
| Unternehmen | 1
|
2
|
3
|
4
|
5
|
6
|
7...25
|
Summe
|
| Umsatz | 1250
|
1000
|
750
|
500
|
300
|
250
|
50
|
5000
|
| Anteil ai | 0,25
|
0,2
|
0,15
|
0,1
|
0,06
|
0,05
|
0,01
|
1
|
| CRj | 0,25
|
0,45
|
0,6
|
0,7
|
0,76
|
0,81
|
...
|
1
|
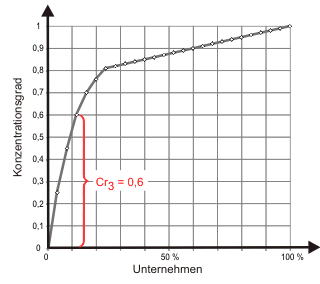 Können sich die Kurven in der Abbildung für verschiedene Industrien schneiden?
Können sich die Kurven in der Abbildung für verschiedene Industrien schneiden?Wie würde die Kurve aussehen, wenn alle Unternehmen einen gleich Umsatz erzielten?
Als CR3 würde also ein Wert von 0,6 ausgewiesen - mit der einfachen Interpretation, dass die drei größten Unternehmen im Markt einen Marktanteil von zusammen 60% besitzen. In Untersuchungen werden üblicherweise die Konzentrationsgrade für die 3, 6, 10, 25, 50 und 100 größten Anbieter ausgewiesen.
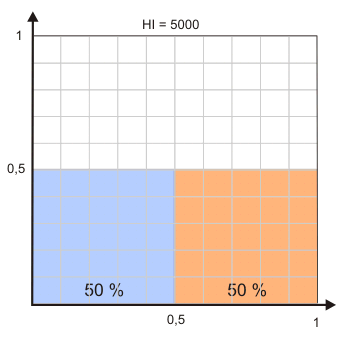
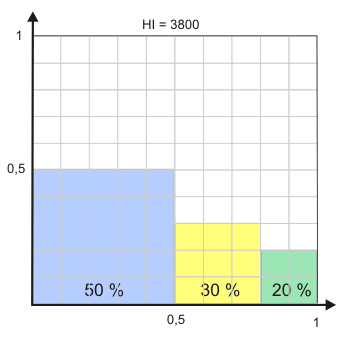
Der entscheidende Kritikpunkt an diesem Maß wird darin gesehen, dass nur die jeweils j größten Unternehmen berücksichtigt werden. Zudem bleibt die relative Konzentration - selbst unter den in den Berechnung eingehenden Unternehmen - außen vor. Ein Maß CR3 = 0,6 wäre auch dann errechnet worden, wenn das größte Unternehmen einen Marktanteil von 50 Prozent und die beiden folgenden jeweils einen Marktanteil von 5 Prozent gehabt hätten. Ebenso hätten die drei größten Unternehmen jeweils einen Marktanteil von 20 Prozent haben können. Hinter gleichen Werten können sich also ganz unterschiedliche Machtverhältnisse der Unternehmen verbergen.
In die Berechnung des (Hirschmann-)Herfindahl-Index HI gehen die Werte aller Unternehmen ein. Er wird berechnet als Summe der quadrierten Anteilswerte
$$ \text{HI} = \sum_{i=1}^n a_i^2 \tag{5} $$Man überlegt leicht, dass der Herfindfahl-Index für ein Monopol den Wert 1 annimmt. Etwas komplizierter ist die Überlegung, welchen kleinsten Wert HI annehmen kann. Da sich die Beziehung
$$ \text{HI} = \cfrac{1}{n} + \cfrac{V^2}{n} \tag{6} $$ableiten lässt*, in der $V$ den Variationskoeffizienten der Daten $x_i$ angibt, kann HI einen Wert von $1/n$ nicht unterschreiten. Dieser kleinste Wert ergibt sich dann, wenn alle Unternehmen gleich groß sind.
$$ \cfrac{1}{n} \le \text{HI} \le 1 \tag{7} $$Die Berechnung in Tabelle 2 setzt das obige Beispiel fort. Da sich mit realen Zahlen oftmals sehr kleine Indexwerte errechnen, werden oft mit dem Faktor 1.000 oder 10.000 multiplizierte Werte ausgewiesen, hier also z.B. 1430. Werte zwischen 1.000 und 1.800 werden als mäßige Konzentration gesehen. Werte unter 1.000 gelten als unbedenklich und solche über 1800 als bedenklich. Ebenso werden bei Werten über 1.000 Unternehmenszusammenschlüsse, die den Index um mehr als 200 Punkte steigen lassen, kritisch eingeschätzt.
| Unternehmen | 1
|
2
|
3
|
4
|
5
|
6
|
7...25
|
Summe
|
| Umsatz | 1250
|
1000
|
750
|
500
|
300
|
250
|
50
|
5000
|
| Anteil ai | 0,25
|
0,2
|
0,15
|
0,1
|
0,06
|
0,05
|
0,01
|
1
|
| ai2 | 0,0625
|
0,04
|
0,0225
|
0,01
|
0,0036
|
0,0025
|
...
|
0,1425
|
Der Kehrwert des Herfindahl-Index entspräche der Zahl der Unternehmen im Markt, wenn alle den gleichen Marktanteil hätten. Dieses Ergebnis kann man unmittelbar in Gleichung (6) ablesen, da der Variationskoeffizient null wäre, wenn keine Größenunterschiede zwischen den Unternehmen (relative Konzentration) zu beobachten wären. Für das Zahlenbeispiel in Tabelle 2 stellt man fest, dass bei ca. 7 gleich großen Unternehmen nach dem Herfindahl-Index dieselbe absolute Konzentration ausgewiesen werden würde. Dieser Wert wird auch als äquivalente Unternehmenszahl bezeichnet oder mit ähnlichen Begriffen belegt. Über einen Indexwert von 0,2 ließe sich also sagen, dass die Konzentration im Markt so ausfällt, als ob es fünf gleich große Oligopolisten gäbe.
Die Quadrierung der Anteilswerte im Herfindahl-Index bewirkt eine stärkere Gewichtung größerer Unternehmen. Das kann man durchaus als Vorteil des Maßes interpretieren, wenn man sich der Auffassung anschließt, dass zwei gleich große Duopolisten ein kleineres Übel für den Wettbewerb darstellen als ein faktischer Monopolist mit einem Marktanteil von 90 Prozent mit einem kleinen Wettbewerber.
Stellt es ein Problem dar, dass bei der Berechnung von CR und HI nur inländische Unternehmen berücksichtigt werden?
Der Herfindahl-Index kann also einfach berechnet und interpretiert werden. Dennoch ist seine Anwendung praktisch nicht unproblematisch. Erste Probleme ergeben sich bereits bei der Abgrenzung des relevanten Marktes. Stehen Fruchtsäfte mit Limonaden in Konkurrenz? Je nachdem wie man diese Frage beantwortet, würde man den Markt weiter oder enger abgrenzen und somit einen niedrigeren oder höheren Herfindahl-Index berechnen. Daneben muss man den Markt z.B. auch regional abgrenzen. Stehen z.B. Fertigbetonanbieter in Nord- und Süddeutschland miteinander in Wettbewerb? Solche Fragen, die man bei einer theoretischen Betrachtung oft schnell aus den Augen verliert oder an die man erst gar nicht denkt, können sich als ernste praktische Probleme erweisen.
Außerdem berücksichtigt der Herfindahl-Index in keiner Weise die vertikale Konzentration der Anbieter. Und es ist ja auch keineswegs gesagt, dass die Wettbewerbsintensität zwischen den Anbietern mit dem Wert des Indexes abnimmt. Der Index sagt schließlich nichts über das Verhalten der Anbieter aus und ist zunächst rein deskriptiv. Eventuell haben sich Anbieter untereinander abgesprochen und verhalten sich quasi wie ein Monopolist. Das kann der Index, der die Zahlen der rechtlich abgegrenzten Unternehmenseinheiten zugrunde legt, natürlich nicht erfassen. Aber man kann ihn sicherlich als Warnsignal einsetzen, indem man Märkte beim Überschreiten kritischer Werte genauer unter die Lupe nimmt.
|
Theoretische Fundierung
Der Herfindahl-Index besitzt noch einen weiteren Vorteil. Mit etwas Mut kann man sagen, dass ein höherer HI-Wert mit einer stärkeren Allokationsverzerrung einhergeht. Zumindest aber ist die Formulierung erlaubt, dass der Index eine gute theoretische Fundierung besitzt.
Um die folgende Ableitung nachvollziehen zu können, sollten Sie vertraut sein mit der Interpretation des Lernerschen Monopolgrads und dem Gleichgewicht im Cournotschen n-pol, mit dem wir uns im Abschnitt über Oligopole befassen werden.
Wie in jedem Unternehmen, ist natürlich auch für einen Oligopolisten Grenzumsatz = Grenzkosten eine notwendige Bedingung für die Gewinnmaximierung. Ist die Nachfrage durch
$$ p=f(X) \space \space \space \text{mit } \space X = \sum_{i=1}^n x_i \tag{8} $$dann lässt sich der Grenzumsatz eines repräsentativen Unternehmens i als
$$ \cfrac{\text{d}U_i}{\text{d}x_i} = p + \cfrac{\text{d}p}{\text{d}X} \cfrac{\text{d}X}{\text{d}x_i} x_i \tag{9} $$angeben. Nach der Cournotschen Verhaltensannahme geht der Anbieter davon aus, dass die Konkurrenten nicht reagieren, wenn er seine Produktionsmenge variiert; also gilt
$$ \cfrac{\text{d}X}{\text{d}x_i} = 1 \tag{10} $$so dass bei n identischen Anbietern
$$ \cfrac{\text{d}U_i}{\text{d}x_i} = p + \cfrac{\text{d}p}{\text{d}X} x_i = p + \cfrac{\text{d}p}{\text{d}X} \cfrac{X}{n} \tag{11} $$mit $E$ für die direkte Preiselastizität der Nachfrage und $a = 1/n$ als Marktanteil eines Anbieters der von ihm erwartete Grenzumsatz als
$$ \cfrac{\text{d}U_i}{\text{d}x_i} = p + \cfrac{\text{d}p}{\text{d}X} \cfrac{X}{n} = p \bigl( 1 + \cfrac{a}{E} \bigr) \tag{12} $$angegeben werden kann. Dieser Ausdruck verallgemeinert die Amoroso-Robinson-Relation auf den n-Anbieter-Fall. Für den Monopolisten wäre a=1 und bei atomistischer Konkurrenz ginge $a$ gegen null, so dass man in (12) bzw. (13) auch die Preis-Grenzkosten-Regel des Konkurrenzanbieters als Spezialfall wiederfindet.
Setzt man nun die Grenzumsätze aus (12) mit den Grenzkosten GK gleich, so erhält man
$$ p \bigl( 1 + \cfrac{a}{E} \bigr) = \text{GK} \tag{13} $$oder umgeformt mit
$$ \text{LR}_n = -\cfrac{a}{E} = \cfrac{p - \text{GK}}{p} \tag{14} $$einen für den n-Anbieterfall verallgemeinerten Lernerschen Monopolgrad.
Wie man - wenig überraschend - in (14) ablesen kann, liegt der Preis um so höher über den Grenzkosten, je größer die Marktanteile ausfallen. Die Interpretation der direkten Preiselastizität der Nachfrage im Hinblick auf die Marktmacht der Anbieter ändert sich gegenüber dem Monopolfall nicht.
Nun ist nur noch zu bedenken, dass der Herfindahl-Index für gleich große Anbieter im Markt dem Kehrwert der Zahl der Unternehmen entspricht; also:
$$ \text{LR}_n = -\cfrac{\text{HI}}{E} = \cfrac{p - \text{GK}}{p} \tag{15} $$Damit lässt sich aussagen, dass die Marktmacht der Anbieter c.p. mit der Konzentration im Markt zunimmt. Je höher der Herfindahl-Index ausfällt, umso höhere Preisaufschläge auf die Grenzkosten und stärkere Allokationsverzerrungen prognostiziert das Cournot-Modell.
Zusammenhang zwischen Herfindahl-Index HI und Variationskoeffizient $V$
$$ \text{HI} = \sum_{i=1}^n (\cfrac{x_i}{X})^2 \tag{1} $$ $$ \text{HI} - \cfrac{1}{n} = \sum_{i=1}^n \Bigl(\cfrac{x_i}{X}\Bigr)^2 - \cfrac{1}{n} \tag{2} $$ $$ \overline{x} = \cfrac{1}{n} \space \space \space \Rightarrow \space \space \space n\overline{x}^2 = \cfrac{1}{n} \tag{3} $$ $$ \text{HI} - \cfrac{1}{n} = \sum_{i=1}^n \Bigl(\cfrac{x_i}{X}\Bigr)^2 - n\overline{x}^2 \tag{4} $$ $$ \text{HI} - \cfrac{1}{n} = \sum_{i=1}^n \Bigl(\cfrac{x_i}{X} - \overline{x}\Bigr)^2 \tag{5} $$ $$ \text{HI} - \cfrac{1}{n} = n\sigma^2 \tag{6} $$ $$ \text{HI} - \cfrac{1}{n} = \cfrac{V^2}{n} \tag{7} $$ $$ \text{HI} = \cfrac{V^2}{n} + \cfrac{1}{n} \tag{8} $$Der Variationskoeffizient ist die mit dem Mittelwert ($1/n$) normierte Standardabweichung: $V = \cfrac{\sigma}{1/n}$. Den Übergang von (4) nach (5) prüft man nach unter Beachtung von $\sum x_i = n\overline{x}$.
Nach ähnlichen Seiten im WWW suchen